Урок 4. Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
\( a_{n-1}a_{n-2}...a_1a_0=a_{n-1} \cdot 8^{n-1} +a_{n-2} \cdot 8^{n-2} +...+a_0 \cdot 8^0 \)
Пример: \( 1063_8=1 \cdot 8^3+ 0 \cdot 8^2+ 6 \cdot 8^1+ 8 \cdot 8^0 =563_{10} \)
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Шестнадцатеричная система счисления называется позиционная система счисления с основанием 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, E, F
\( 3AF_{16}=3 \cdot 16^2+ 10 \cdot 16^1+ 15 \cdot 16^0=768+160+15=943_{10} \)
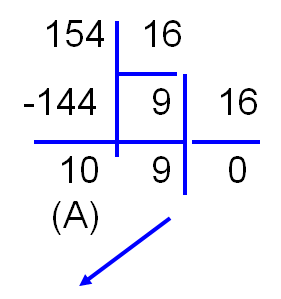
Переведём десятичное число 154 в шестнадцатеричную систему счисления: