Урок 5. Правило перевода целых десятичных чисел в систему счисления с основанием q
Система
счисления —
это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит - совокупность цифр системы счисления.
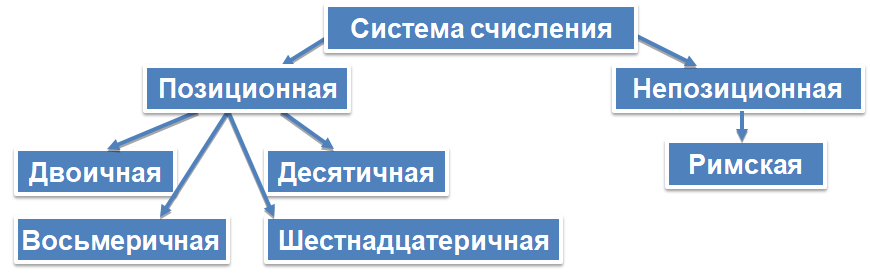
Система
счисления называется позиционной,
если количественный эквивалент цифры в числе зависит от её положения в записи
числа.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
\( A_q=\pm (a_{n-1} \cdot q^{n-1}+a_{n-2} \cdot q^{n-2}+...+a_0 \cdot q^0+a_{-1} \cdot q^{-1}+...+a_{-m} \cdot q^{-m}) \)
Здесь:
А — число;
q — основание системы счисления;
\( a_i \) — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
\( q_i \) — «вес» i-го разряда.